

R = distance between axis and rotation mass (in. Moment of Inertia Calculation Formula Moment of Inertia of a Hollow Cylinder M (D2 + d2 ) kgm2. I = ∑ i m i R i 2 = m 1 R 1 2 + m 2 R 2 2 +. The moment of all other moments of inertia of an object are calculated from the the sum of the moments.

R = distance between axis and rotation mass (ft, m) Where: m mass of the hollow (lb m, kg) R distance between axis and the thin walled hollow (ft, m) Thin Wall Shaft Mass Moment of Inertia Calculator Hollow Cylinder. I = moment of inertia (lb m ft 2, kg m 2 ) Thin-walled hollow cylinder: Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass and can be expressed as: I m R 2. Solid Square Cross Section The Area Moment of Inertia for a solid square section can be calculated as I x a 4 / 12 (2) where a side (mm, m, in. Second Moment of Area (or moment of inertia) of a. Radius of Gyration in Structural Engineering Some Typical Bodies and their Moments of Inertia Cylinder Thin-walled hollow cylinder. A hollow cylinder with mass M, internal radius R1, and external radius R2 rotates on an axis that runs through the centre of the cylinder and has a moment of inertia specified by the formula: I is equal to (1/2)M(R12 + R22) Note: You may find the formula for the moment of inertia of a hollow thin-walled cylinder by setting R1 R2 R (or, more. Using the structural engineering calculator located at the top of the page (simply click on the the 'show/hide calculator' button) the following properties can be calculated: Area of a Hollow Circle or Annulus. Point mass m (mass) at a distance r from the axis of rotation. I moment of inertia for the body (kg m 2, slug ft 2) m mass of the body (kg, slugs) vs. The moment of inertia about the axis x1 through the vertex, perpendicular to the central. and moment of inertia I(dz) 1 2m(dz)r2 : 0h 1 2(Rz h)4 dz 1 10R4h 3 10MR2. The Moment of Inertia of a Hollow Sphere, otherwise called a spherical shell, is determined often by the formula that is given below. The moment of inertia about the central axis of the cone is (taking density ) that of a stack of discs each having mass. Geometrically simple objects have moments of inertia that can be expressed mathematically, but it may not be straightforward to symbolically express the moment of inertia of more complex bodies. The Moment of Inertia that belongs to a rigid composite system is given by the sum of Moments of Inertia of its component subsystems (all taken about the same Axis). It should not be confused with the second moment of area, which is used in bending calculations. EDIT: J is the polar moment of inertia of the area, not the mass. I think you can take it from there to find the connection. I have included an image of this below: Moreover, in order to obtain the moment of inertia for a thin cylindrical shell (otherwise known as a hoop), we can substitute R1 R2 R, as the shell has a negligible thickness. The mass of the cylinder is given by m V m V, and the volume of a cylinder is V LA V L A, where L L is the height (or length) of the cylinder and A r2 A r 2, the cross sectional area. Here, we can avoid the steps for calculation as all elemental masses composing the cylinder are at a xed (constant) distance 'R' from the axis. Mass moments of inertia have units of dimension mass × length 2. By setting R1 0, we can therefore work out the specific moment of inertia equation for a solid cylinder. 2.5 Moment of inertia of a hollow cylinder about its axis The gure here shows the small element with repect to the axis of rotation. Example 6: When r 1 is 10 m, r 2 is 20 m, and the mass of the annular ring is 14 kg, calculate the moment of inertia of the ring.
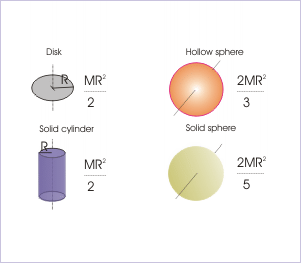
We have for hollow cylinder, MOI (I) MR 2. stands in contact against the inner wall of a hollow cylindrical drum of. Example 5: If the mass is 10 kg and the radius is 7 m, determine the hollow cylinder’s moment of inertia. The mass moment of inertia, usually denoted I, measures the extent to which an object resists rotational acceleration about an axis, and is the rotational analogue to mass. (b) The moment the stone is dropped from the car, horizontal force on the stone. This holds true for all regular polygons.Related Resources: mechanics machines Mass Moment of Inertia Equations The result is valid for both a horizontal and a vertical axis through the centroid, and therefore is also valid for an axis with arbitrary direction that passes through the origin.


 0 kommentar(er)
0 kommentar(er)
